[python] Numpy Dimension, Axis

도입

Numpy를 사용한지 얼마되지 않았다면 Axis와 Broadcasting 때문에 머리가 아플때가 많다. (필자도 가끔씩 골머리 썩고 있다)

배열 접근이나 연산(dot product, sum 등..) 시에 지금 연산하고자 하는 축이 어디인지..

자주 하다보면 직감으로 되지만, 그렇지 않다면 예외를 만나기 일쑤다.

Axis? Dimension?

삽질해보겠다고, 예제를 만들 때 더욱 헷갈리게 만드는 행동 중 하나가 있다.

바로 같은 데이터, 같은 길이로 예제 데이터를 작성하는 것이다.

Axis와 Dimension에 대한 직관적인 예를 하나 준비했다.

그런데, 그 전에 앞서 Dimension에 대해 조금만 알고 가자.

1)

x = np.array([1,2,3,4,5])

이 데이터는 몇차원 데이터인가?

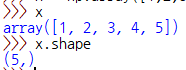
보나마나 1차원에, 5개 요소를 가진 배열이다.

2)

x = np.array( [[1,2,3,4,5], [6,7,8,9,10]] )

오 순간 흠칫했다.

중첩대괄호가 2개(Nested)이니 당연히 2차원 데이터다.

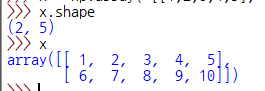
어 그런데 x.shape이 5,2가 아니라 2,5다!  2×5(2행 5열 크기) 형태의 배열이기 때문이다.

3)

이제 말하고 싶은 내용을 전할 차례이다.

1)의 데이터는 1×5일까? 5×1일까?

“1×5지” 라고 하면 아니올시다.

갑자기 골아프다면 너무 걱정하지말고, 다음 설명을 천천히 읽어보자

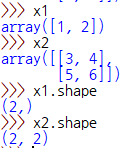
행렬의 내적은 AxB * BxC 일때 AxC 형태를 갖는다.

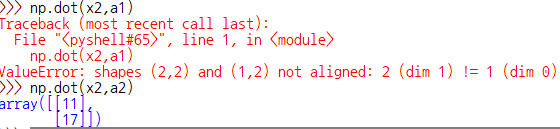
가. 2×1일 경우

(2×1) * (2×2) => 연산 불가

단, 반대로 내적시

(2×2) * (2×1) => (2×1) 로 가능.

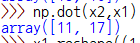
따라서 np.dot(x2,x1) 시에 연산이 가능! 결과도 [11,17]로 일치한다.

나. 1×2일 경우

(1×2) * (2×2) => (1×2)

np.dot(x1,x2) 시에 연산이 가능! 결과가 [13,16]으로 맞다! ….. ? ?????

다시 말해 (2,) 라는 형태는 (1,2)도 되고 (2,1)도 된다. 이는 Numpy의 똑똑함(공밀레) 덕분에 가능한 일이다. 그렇기 때문에 답은 1×2, 2×1 둘 다 이다.

4)

뿐만 아니라, 명시적으로도 형태 지정이 가능하다.

이 경우 위의 3)의 예제를 다시 대입하면,

가. 2×1의 경우

( a1.shape = (1,2) / a2.shape = (2,1) )

x2 * a2인 (2×2) * (2×1)는 가능!

x2 * a1인 (2×2) * (1×2)는 불가능 되시겠다.

나. 1×2의 경우

( a1.shape = (1,2) / a2.shape = (2,1) )

a1 * x2인 (1×2) * (2×2)는 가능!

a2 * x2인 (2×1) * (2×2)는 불가능!

본격 Axis

위까지 이해를 했다면, 본격적으로 Axis에 대한 설명을 진행해도 좋다고 생각한다.

4차원 배열(ndarray) 하나가 있다. 

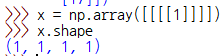
이 4차원 배열에서 1차원 데이터가 1개 있다. ( 1을 담고있는 [1])

2차원 데이터도 1개이고( [1]을 담고있는 [[1]])

3차원은 1개, ([[1]]을 담고있는 [[[1]]])

4차원은 1개이다.  ([[[1]]] 을 담고있는 [[[[1]]]])

진짜 제대로 된 아래의 예시를 보자.

import numpy as np
from pprint import pprint
x = np.array([[[1,1,1,1],[2,2,2,2],[3,3,3,3]], [[4,4,4,4],[5,5,5,5],[6,6,6,6]]])

print("[Data] X :")
pprint(x)
print("[Shape] X :")
pprint(x.shape)
print("---------------------------------------")

s0 = np.sum(x, axis=0)
print("[Data] s0 :")
pprint(s0)
print("[Shape] s0 :")
pprint(s0.shape)
print("---------------------------------------")


s1 = np.sum(x, axis=1)
print("[Data] s1 :")
pprint(s1)
print("[Shape] s1 :")
pprint(s1.shape)
print("---------------------------------------")


s2 = np.sum(x, axis=2)
print("[Data] s2 :")
pprint(s2)
print("[Shape] s2 :")
pprint(s2.shape)
print("---------------------------------------")

그런데 우리는 가장 큰 차원인 axis=0을 없앴기 때문에 2,3,4에서 2를 없앤 3,4형태가 나오게 더해야한다. 다음과 같이 말이다.

그 결과 내부는 3,4의 shape형태를 띄고있고, 가장 바깥에 [ ] 로 감싸어져 있는것을 볼 수 있다.

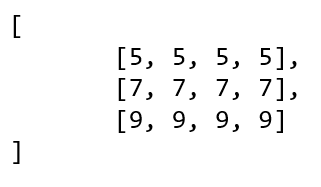
s1은 axis=1로 x를 summation한 결과이다.

가장 바깥쪽 축에서 하나 안에 있는 축을 기준으로 더하게 된다.

1차원 원소 4개를 가진 배열이 2개 있는 (2,4)형태의 배열이 됐다.

s2는 axis=2로 x를 sumaation했다.

가장 바깥쪽에서 시작해서 안에있는, 또 그 안에 있는 축을 기준으로 더하자.

글을 마치며…

사실 이렇게 길게 쓰려고 한 생각은 없었는데, 중간 설명과 사진이 포함되다보니 점점 길어진 것 같다.

오히려 이해에 독이 됐을까 걱정이 되지만 그림과 함께 최대한 쉽게 설명을했으니 “차근차근”만 읽어본다면 이해에 무리가 없을 것이다.

부디 기계학습이나 인공지능 제작과정에서 axis때문에 골머리를 썩히지 않길 바란다..

추후 브로드캐스팅(Broad Casting)에 대해서도 포스트를 남길 예정이다.